Entfernungsberechnung
 Mit der wachsenden Verbreitung von GPS Geräten und Tools wie Google Earth oder GeoPosition ist es ein leichtes, die geografischen Koordinaten von interessanten Punkten auf der Erdoberfläche zu bestimmen. Wie man mittels dieser Koordinaten die exakte Luftlinienentfernung zwischen zwei Punkten bestimmt, zeigt dieser Artikel.
Mit der wachsenden Verbreitung von GPS Geräten und Tools wie Google Earth oder GeoPosition ist es ein leichtes, die geografischen Koordinaten von interessanten Punkten auf der Erdoberfläche zu bestimmen. Wie man mittels dieser Koordinaten die exakte Luftlinienentfernung zwischen zwei Punkten bestimmt, zeigt dieser Artikel.
Hinweis: Zur Darstellung von Dezimalzahlen wird in diesem Artikel die englische Notation benutzt, das heißt das Dezimaltrennzeichen ist der Punkt.
Geografische Koordinaten
Die Erdoberfläche ähnelt der Oberfläche einer Kugel. Jeder Punkt auf der Erdoberfläche kann damit durch zwei Koordinaten eindeutig beschrieben werden: Länge und Breite.
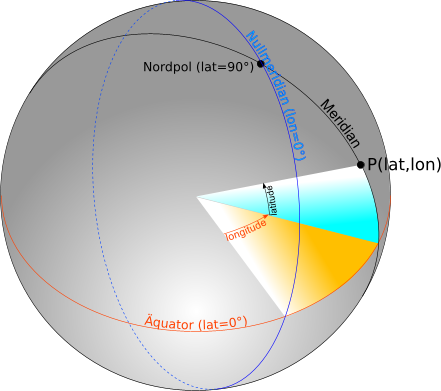
Die geografische Breite (englisch: Latitude, abgekürzt: lat) beschreibt den Winkel, der sich zwischen Erdmittelpunkt, dem gesuchten Punkt P und dem Äquator aufspannt (blaue Fläche in Abb. 1). Punkte auf dem Äquator haben immer die Breite 0, während der Nordpol 90 Grad und der Südpol -90 Grad geografische Breite haben. Die Kurve, die durch Punkte gleicher Breite führt, bezeichnet man als Breitenkreis.
Die geografische Länge (englisch: Longitude, abgekürzt: lon) bezeichnet den Winkel, der sich zwischen Erdmittelpunkt, dem gesuchten Punkt P und dem Nullmeridian ergibt (gelbe Fläche in Abb. 1). Ein Meridian oder Längenkreis führt durch Nordpol, Südpol und alle Punkte gleicher Länge. Der Meridian, der durch die alte Greenwicher Sternwarte führt, bekam willkürlich den Wert 0 zugewiesen und ist somit der Nullmeridian. Punkte östlich von Greenwich haben eine Länge zwischen 0 und 180 Grad, westlich davon zwischen 0 und -180 Grad. Die Meridiane -180 und 180 Grad sind identisch und stellen quasi die Verlängerung des Nullmeridians dar.
Beispiele für geografische Koordinaten
| Ort | Breite | Länge in Grad |
|---|---|---|
| Rüsselsheim Bahnhof | 49.9917 | 8.41321 |
| Rüsselsheim Opelbrücke | 50.0049 | 8.42182 |
| Berlin Brandenburger Tor | 52.5164 | 13.3777 |
| Lissabon Tejo Brücke | 38.692668 | -9.177944 |
Einfachste Entfernungsberechnung
Als erstes soll die Entfernung zwischen Rüsselsheim Bahnhof und Opelbrücke bestimmt werden. Die einfachste Variante ist, zunächst eine Karte von Rüsselsheim mit eingezeichneten Längen- und Breitenkreisen zur Hand zu nehmen (Abb. 2).
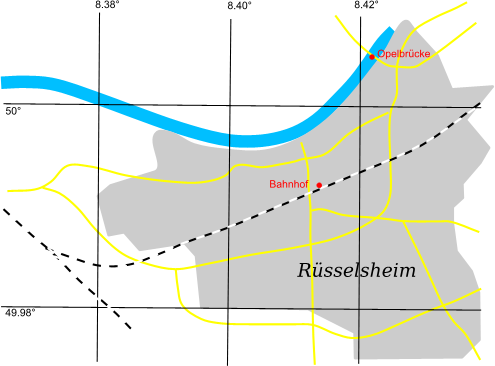
Wie man sieht, stellen auf der Karte die Längen- und Breitenkreise gerade Linien dar und verlaufen parallel beziehungsweise rechtwinklig zueinander. Man kann daher zur Entfernungsbestimmung für dieses relativ kleine Gebiet einfach die Erdoberfläche als Ebene ansehen und zum Satz des Pythagoras greifen:
distance = sqrt(dx * dx + dy * dy)
mit distance: Entfernung in km
dx = 71.5 * (lon1 - lon2)
dy = 111.3 * (lat1 - lat2)
lat1, lat2, lon1, lon2: Breite, Länge in Grad
Wenn man Länge und Breite in Grad angibt, ergibt sich die Entfernung in Kilometern. Die Konstante 111.3 ist dabei der Abstand zwischen zwei Breitenkreisen in km und 71.5 der durchschnittliche Abstand zwischen zwei Längenkreisen in unseren Breiten. (Genauer gesagt sind 111.3 km 1 Grad auf dem Äquator des Hayford-Ellipsoiden).
Verbesserte Methode
Während der Abstand zwischen zwei Breitenkreisen immer konstant 111.3 km beträgt, variiert der Abstand zwischen zwei Längenkreisen in Abhängigkeit von der geografischen Breite: Am Äquator ist er ebenfalls 111.3 km, an den Polen hingegen 0. Genauer gesagt berechnet sich der Abstand nach der Formel
111.3 * cos(lat)
Dies lässt sich in die Berechnungsformel mit einarbeiten. Als Wert für lat wird dabei ein Wert gewählt, der genau zwischen lat1 und lat2 liegt.
Bei der Berechnung mittels eines Computers ist zu bedenken, dass die meisten Programmiersprachen zwar die Kosinusfunktion zur Verfügung stellen, diese in der Regel den Winkel jedoch im Bogenmaß (Radiant) erwartet. Die Umrechnung von Grad in Radiant erfolgt nach der Beziehung:
1° = π/180 rad ≈ 0.01745
Die vollständige, verbesserte Formel zur Entfernungsberechnung lautet dann:
distance = sqrt(dx * dx + dy * dy) mit distance: Entfernung in km dx = 111.3 * cos(lat) * (lon1 - lon2) lat = (lat1 + lat2) / 2 * 0.01745 dy = 111.3 * (lat1 - lat2) lat1, lat2, lon1, lon2: Breite, Länge in Grad
Exakte Entfernungsberechnung für die Kugeloberfläche
Leider versagen diese einfachen Methoden bei größeren Entfernungen. Der Grund dafür leuchtet ein, wenn man zum Beispiel eine Europakarte betrachtet (Abb. 3):
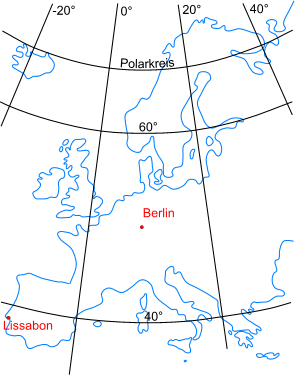
Die Längen- und Breitenkreise bilden hier kein rechtwinkliges Gitternetz mehr. Die Ursache dafür ist die kugelförmige Gestalt der Erde. Es ist aber unmöglich, eine Kugeloberfläche verzerrungsfrei in eine Ebene abzurollen. Während man die Verzerrung auf kleinen Karten wie einem Stadtplan noch ignorieren kann, lässt sich eine Europakarte auf diese Art und Weise nicht mehr herstellen.
Man muss hier zu Methoden der sphärischen Trigonometrie greifen und das eingangs zur Definition von Länge und Breite Gesagte berücksichtigen.
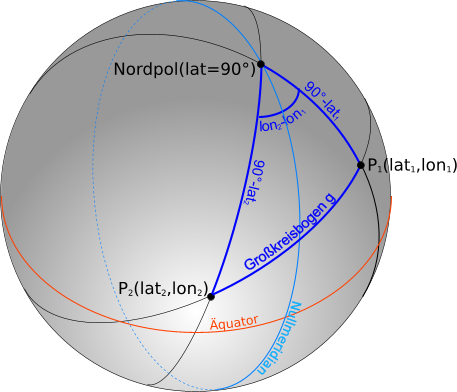
Abb. 4 zeigt nochmals die Erde als Kugel, jetzt aber mit zwei eingezeichneten Punkten P1 und P2, deren Abstand bestimmt werden soll. Diesen (kürzesten) Abstand bezeichnet man auch als Großkreisbogen. Die Punkte P1 und P2 bilden zusammen mit dem Nordpol ein Kugeldreieck. Von diesem sind zwei Seiten und der von ihnen eingeschlossene Winkel bekannt: Die Seitenlänge ist gleich dem Abstand des Punktes vom Nordpol, also 90 Grad minus seine geografische Breite. Der eingeschlossene Winkel berechnet sich aus der Differenz der geografischen Längen der beiden Punkte.
Damit ist es jetzt möglich, die Länge der dritten Seite zu bestimmen, die den gesuchten Großkreisbogen darstellt. Zur Anwendung kommt der Seitenkosinussatz:
cos(g) = cos(90° - lat1) * cos(90° - lat2) + sin(90° - lat1) * sin(90° - lat2) * cos(lon2 - lon1) mit g: Gesuchter Großkreisbogen lat1, lat2, lon1, lon2: Breite, Länge
Da cos(90° - a) = sin(a) und sin(90° - a) = cos(a) gilt, vereinfacht sich die Formel zu:
cos(g) = sin(lat1) * sin(lat2) + cos(lat1) * cos(lat2) * cos(lon2 - lon1)
Um die Entfernung in Kilometern zu bekommen, muss man noch den Arkuskosinus bilden und das Ergebnis mit dem Erdradius multiplizieren:
dist = 6378.388 * acos(sin(lat1) * sin(lat2) + cos(lat1) * cos(lat2) * cos(lon2 - lon1)) mit dist: Entfernung in km
(Der Wert für den Erdradius entspricht hier der großen Halbachse des Hayford-Ellipsoiden).
Die Formel gilt für die Angabe der Winkel in Radiant, was für die meisten Programmiersprachen der Standard ist. Rechnet man dagegen mit einem Taschenrechner, der auf Grad eingestellt ist, dann ist statt 6378.388 der Wert 6378.388 * π / 180 = 111.324 zu verwenden.
Berechnung mit der Haversine Formel
Die Berechnungsformel nach dem Kugeldreieck ist zwar mathematisch korrekt, führt aber bei sehr geringen Enfernungen unter einem Meter zu fehlerhaften Ergebnissen. Die Ursache ist, dass Computer in der Regel nicht mit beliebiger Genauigkeit rechnen, sondern zum Beispiel bei der Verwendung des C++ Datentyps double die Genauigkeit auf 15 signifikante Digits begrenzt ist. Das führt bei geringen Entfernungen dazu, dass aufgrund von Rundungsfehlern das Ergebnis immer Null ist.
Zu besseren Ergebnissen führt hier die Haversine Formel, die ebenfalls die mathematisch korrekte Entfernung auf der Kugeloberfläche berechnet, aber bei kleinen Entfernungen eine bessere numerische Kondition aufweist:
dLat = lat2-lat1 dLon = lon2-lon1; a = pow(sin(dLat/2.0), 2) + pow(sin(dLon/2.0), 2) * cos(lat1) * cos(lat2) dist = 6378.388 * 2.0 * atan2(sqrt(a), sqrt(1.0-a)) mit dist: Entfernung in km
Bewertung der Methoden
Welche der vier vorgestellten Methoden nun zu Anwendung kommt, hängt von diversen Faktoren ab:
- Entfernung der Punkte
- Geforderte Genauigkeit
- Kosten der Berechnung (d.h. Verbrauch von Zeit, CPU-Zyklen, ...)
Auf schnellen PCs ist die Frage der Kostenunterschiede mittlerweile nicht mehr so relevant. Muss man die Formeln aber jedesmal auf dem Taschenrechner eintippen, spielt der Zeitaufwand schon ein große Rolle.
Zum Vergleich der Genauigkeit werden nun die Formeln für die Bestimmung der Entfernung zwischen Rüsselsheim Bahnhof und Opelbrücke, zwischen Berlin und Lissabon sowie zwischen zwei Punkten mit 1 Meter beziehungsweise 1 Centimeter Abstand durchgerechnet.
| Strecke | Einfach | Verbessert | Seitenkosinussatz | Haversine |
|---|---|---|---|---|
| Rüsselsheim Bahnhof - Rüsselsheim Opelbrücke | 1.593 km | 1.593 km | 1.593 km | 1.593 km |
| Berlin Brandenburger Tor - Lissabon Tejo Brücke | 2228.929 km | 2334.931 km | 2317.722 km | 2317.722 km |
| Entfernung 1 m | 0.001000 km | 0.001000 km | 0.001001 km | 0.001000 km |
| Entfernung 1 cm | 0.000010 km | 0.000010 km | 0.000000 km | 0.000010 km |
Die Berechnungen erfolgten mit einem in C++ geschriebenen Programm (Sourcecode auf GitHub).
Für Entfernungen im Bereich einiger Meter bis Kilometer sind die vier Varianten von ihrer Genauigkeit her praktisch gleichwertig. Bei Entfernungen im europäischen Maßstab ergeben sich aber große Unterschiede, so dass man hier immer die genauen Methoden mit Berücksichtigung der Kugeloberfläche verwenden sollte. Für sehr geringe Entfernungen im Bereich unterhalb eines Meters weist die Berechnung nach dem Seitenkosinussatz eine numerische Instabilität auf, die zu falschen Ergebnissen führt. Die Haversine Formel liefert sowohl bei großen als auch sehr geringen Entfernungen ein korrektes Ergebnis und stellt damit das Optimum dar.
Ergänzung 1: Entfernungsberechnung für Ellipsoide
Die bisherigen Überlegungen sind immer davon ausgegangen, dass die Erde eine Kugel ist. Das ist jedoch nicht der Fall. Sie stellt vielmehr ein unregelmäßig geformtes Geoid dar. Am ehesten lässt sich diese Gestalt noch durch ein Rotationsellipsoid annähern. Ein Rotationsellipsoid wird durch zwei Radien bestimmt, daher findet man in den meisten Tafelwerken auch zwei Werte für den Erdradius: Am Äquator und am Pol.
Leider gibt es für das Ellipsoid keine einfache Formel analog zum Seitenkosinussatz für die Kugel. Die Berechnung von Entfernungen auf der Oberfläche eines Ellipsoids ist wesentlich komplizierter. Außerdem gibt es nicht «das Erdellipsoid», sondern Dutzende davon. Jenachdem, an welcher Stelle der Erdoberfläche man sich befindet, kommt man nämlich zu unterschiedlichen Ergebnissen für die optimalen Ellipsoidparameter, um eine möglichst gute Annäherung an die wirkliche Erdoberfläche zu erzielen. Diese Ellipsoidparameter (große und kleine Halbachse, Verschiebung des Mittelpunktes) fasst man oft unter dem Begriff «Kartendatum» oder «geodätisches Datum» zusammen, von denen es einige hundert verschiedene gibt. Eine de facto Vereinheitlichung wurde erst durch die Verbreitung des weltumspannenden Global Positioning Systems (GPS) erreicht, welches das Referenzellipsoid WGS84 verwendet.
Die Entwicklung eines Tools zur exakten Entfernungsbestimmung für alle möglichen Ellipsoide und Kartendatums ist also doch eine komplexere Angelegenheit. Zum Glück gibt es solche Tools aber schon, in diesem Artikel soll PROJ.4 - Cartographic Projections Library das Tool der Wahl sein. Proj.4 liegt komplett im Sourcecode und als Binärdistribution für Linux und Windows vor. Außerdem gibt es mit der Java Map Projection Library eine teilweise Portierung von Proj.4 auf Java.
Zur Entfernungsberechnung dient das im Paket enthaltene Kommandozeilenprogramm geod. Der Aufruf
geod +ellps=WGS84 +units=km -I
erwartet dann die Eingabe der Koordinaten der beiden Punkte im Format lat1 lon1 lat2 lon2 als Dezimalgrad, zum Beispiel
49.9917 8.41321 50.0049 8.42182
Der letzte Wert der Ausgabe ist dann die Entfernung in Kilometern. Zur Berechnung wird das WGS84 Ellipsoid verwendet, das heißt die eingegebenen Koordinaten müssen im dem WGS84 System bestimmt worden. Für die originalen GPS-Koordinaten ist das immer der Fall, sofern nicht das GPS-Gerät selbst schon eine Koordinatentransformation vornimmt.
Bei der Überprüfung des Beispiels ergibt sich für die kurze Entfernung in Rüsselsheim wieder 1.593 km. Die Entfernung Berlin - Lissabon wird jetzt mit 2318.217 km berechnet. Die Kugelmethode liegt also etwa 500 Meter daneben, was auf die große Entfernung bezogen gerade mal einen Fehler von 0.02% bedeutet.
Ergänzung 2: Benutzung anderer Kartengitter
Die vereinfachten Methoden der ebenen Trigonometrie reichen zur Bestimmung kurzer Entfernungen also völlig aus. Ein Manko der angegebenen Formeln ist allerdings die Notwendigkeit, mit den «krummen» Werten für die Abstände der Längen- und Breitenkreise multiplizieren müssen. Darüber hinaus sind die Abstände der Längenkreise nicht konstant. Viel schöner wäre es, wenn man Koordinaten zur Verfügung hätte, die diese Nachteile nicht haben, also direkt in Entfernungsangaben umgerechnet werden können.
Solche Koordinatensysteme gibt es natürlich schon. Die bekanntesten sind in Europa das Gauß-Krüger-Koordinatensystem und weltweit das UTM-Koordinatensystem. Beide Koordinatensysteme erlauben es, kleine Gebiete so abzubilden, dass sie mit einem rechtwinkligen Koordinatensystem überzogen werden können.
Diese Koordinaten werden dann nicht mehr in Grad gemessen, sondern in Metern. Statt Breite und Länge tragen sie meist die Bezeichnung Hochwert und Rechtswert oder Northing und Easting.
Das Tool GeoPosition erlaubt die Umrechnung von geografischen in UTM Koordinaten. Für die beiden bekannten Orte in Rüsselsheim ergibt sich:
| Ort | Rechtswert | Hochwert UTM Zone 32U |
|---|---|---|
| Rüsselsheim Bahnhof | 457939 m | 5537873 m |
| Rüsselsheim Opelbrücke | 458568 m | 5539336 m |
Da die Koordinaten in Metern angegeben sind und in der gleichen UTM Zone liegen, kann man die Entfernung sofort mit dem Satz des Pythagoras ausrechnen und es ergibt sich wieder der bekannte Wert von 1.593 km.
Tatsächlich sind diese Koordinaten so bequem zu verwenden, dass die meisten topografischen Karten, die ja nur ein relativ kleines Gebiet abbilden, ein UTM-Koordinatensystem statt «krummer» geografischer Koordinaten aufgedruckt haben.